[論文メモ] Recommendations as Treatments: Debiasing Learning and Evaluation

こんにちは、さとうみなとです。Explicit feedbackにおける推薦システムにおいてバイアス除去を試みた論文の一部追試をしたので部分的に紹介します。

• タイトル：Recommendations as Treatments: Debiasing Learning and Evaluation
• 著者：Tobias Schnabel, Adith Swaminathan, Ashudeep Singh, Navin Chandak, Thorsten Joachims
• 所属：Cornell University
• 発表会議：ICML 2016

概要

推薦システムを学習、評価するためのデータセットの多くは推薦システムの過去の推薦方策やユーザーの自己選択による選択バイアス(selection bias)の影響を受けている。 本研究ではそういった選択バイアスに対処するための因果推論に基づく手法を提案する。

導入

Notation

• ユーザー：$u \in\{1, \ldots, U\}$
• アイテム：$i \in\{1, \ldots, I\}$
• 評価値の行列：$Y \in \Re^{U \times I}$

MCARとMNARについて

Missing Completely At Random (MCAR)

現実的に得られる評価値の行列 $Y$ はすべての要素が埋められているわけではない。埋められていない値=欠損値が完全にランダムに生じているようなケースをMCARというらしい。 ただこれについても、推薦システムの過去の推薦方策やユーザーの自己選択による選択バイアスがあるため、現実的に得るのは困難だと思われる。

Missing Not At Random (MNAR)

評価値行列 $Y$ の欠損値の有無は、$Y$ 以外の他の変数(ユーザー/アイテム)だけでなく、$Y$ 自身と関係しているケースをMNARというらしい。 例を出すと、Popularityの高いアイテムにはたくさんの評価が付きやすい(= $Y_{*,i}$ が観測されやすい)し、ユーザーは恣意的に評価したいものを選んで評価する傾向があるのでMCARで得られるデータよりも評価値が高い傾向にある(みんな好き好んで興味のないアイテムの評価をしたがらないですよね)。

後ほど登場するYahoo! R3 DatasetはtrainはMNAR、testはMCARなデータとなっている。

損失について

真の損失

ユーザーのアイテムに対する評価値の予測集合 $\hat{Y}$ に対する真の損失は

$R(\hat{Y})=\frac{1}{U \cdot I} \sum_{u=1}^{U} \sum_{i=1}^{I} \delta_{u, i}(Y, \hat{Y})$

と定式化できる。ここで $\delta_{u, i}(Y, \hat{Y})$ はユーザー $u$ のアイテム $i$ に対する予測値の局所損失を表すが、下記のようなものがあげられる。

• MAE : $\delta_{u, i}(Y, \hat{Y}) = \left|Y_{u, i}-\hat{Y}_{u, i}\right|$
• MSE : $\delta_{u, i}(Y, \hat{Y}) = \left(Y_{u, i}-\hat{Y}_{u, i}\right)^{2}$
• Accuracy: $\delta_{u, i}(Y, \hat{Y}) = \mathbf{1}\left\{\hat{Y}_{u, i}=Y_{u, i}\right\}$

ナイーブな推定量

実際のところ $Y$ は部分的にしか観測することができない。 そこで、ユーザー $u$ のアイテム $i$ に対する評価値 $Y_{u,i}$ が観測できたかどうかを表す確率変数 $O_{u, i}$ を導入して、$Y$ の中で観測できたもので平均をとる

$\hat{R}_{\text {naive}}(\hat{Y})=\frac{1}{\left|\left\{(u, i): O_{u, i}=1\right\}\right|} \sum_{(u, i): O_{u, i}=1} \delta_{u, i}(Y, \hat{Y})$

がナイーブな推定量として用いられる。しかしこれについて期待値をとると、

$\mathbb{E}_{O}\left[\hat{R}_{\text {naive}}(\hat{Y})\right] \neq R(\hat{Y})$

となる(不偏推定量と一致しない)。

IPS推定量

$Y_{u,i}$ が観測される確率 $P_{u,i} = P(O_{u,i} = 1)$ を Propensityといい、すべてのユーザー/アイテムについて非ゼロであると仮定する。

IPS推定量とは、このPropensity $P_{u,i}$ の逆数で重み付けを行う推定量(Inverse-Propensity-Scoring estimator)のことをいう。

$\hat{R}_{I P S}(\hat{Y} | P)=\frac{1}{U \cdot I} \sum_{(u, i): O_{u, i}=1} \frac{\delta_{u, i}(Y, \hat{Y})}{P_{u, i}}$

これについて期待値をとると（当然そのように設計しているので）

$\begin{aligned} \mathbb{E}_{O}\left[\hat{R}_{I P S}(\hat{Y} | P)\right] &=\frac{1}{U \cdot I} \sum_{u} \sum_{i} \mathbb{E}_{O_{u, i}}\left[\frac{\delta_{u, i}(Y, \hat{Y})}{P_{u, i}} O_{u, i}\right] \\ &=\frac{1}{U \cdot I} \sum_{u} \sum_{i} \delta_{u, i}(Y, \hat{Y})=R(\hat{Y}) \end{aligned}$

となる(不偏推定量と一致する)。

SNIPS推定量

IPS推定量の分散を抑えるために $\mathbb{E}_{O}\left[\sum_{(u, i): O_{u, i}=1} \frac{1}{P_{u, i}}\right]=U \cdot I$ であることを利用した、

$\hat{R}_{S N I P S}(\hat{Y} | P)=\frac{\sum_{(u, i): O_{u, i}=1} \frac{\delta_{u, i}(Y, \hat{Y})}{P_{u, i}}}{\sum_{(u, i): O_{u, i}=1} \frac{1}{P_{u, i}}}$

をSNIPS推定量(Self-Normalized Inverse Propensity Scoring estimator)という。

ナイーブベイズを用いたPropensityの推定

ナイーブベイズを用いたPropensityの推定は下記の式で表される。

$P\left(O_{u, i}=1 | Y_{u, i}=r\right)=\frac{\overbrace{P(Y=r | O=1) P(O=1)}^{\text{(1) from MNAR data}}}{\underbrace{P(Y=r)}_{\text{(2) from a small sample of MCAR data.}}}$

式中の(1)はPropensityを予測したい対象のMNARなデータを集計すれば簡単に求まる一方、(2)はMCARなデータから求める必要がある。。。

実験(追試)

データセット

実験に用いたのは楽曲の評価データセットであるYahoo! R3 Datasetで、こちらはtrainはMNARである一方、testはMCARであるのがポイント。 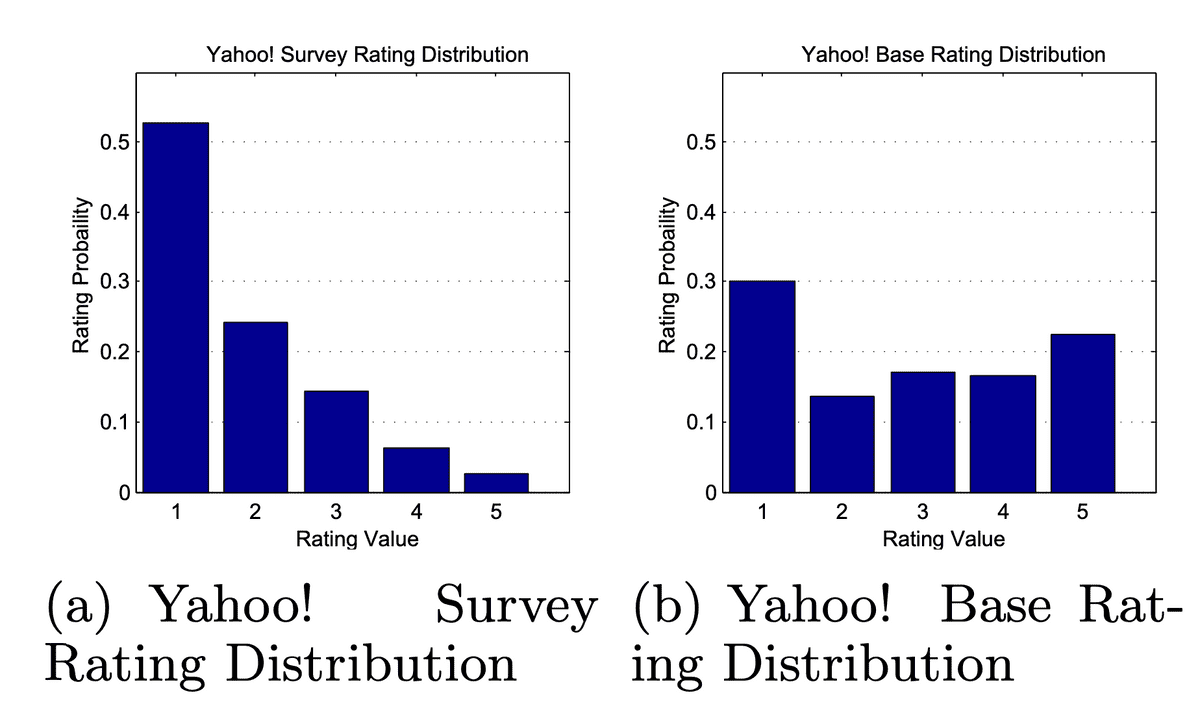[Marlin et al. 2007]

ご覧の通りtrainとtestの評価値の分布が大きく異なっていることがわかる。今回の実験ではYahoo! R3 Datasetのtestから5%サンプリングしてPropensityの推定に用い、残りの95%を真の意味でのtestとして用いている。

実験結果

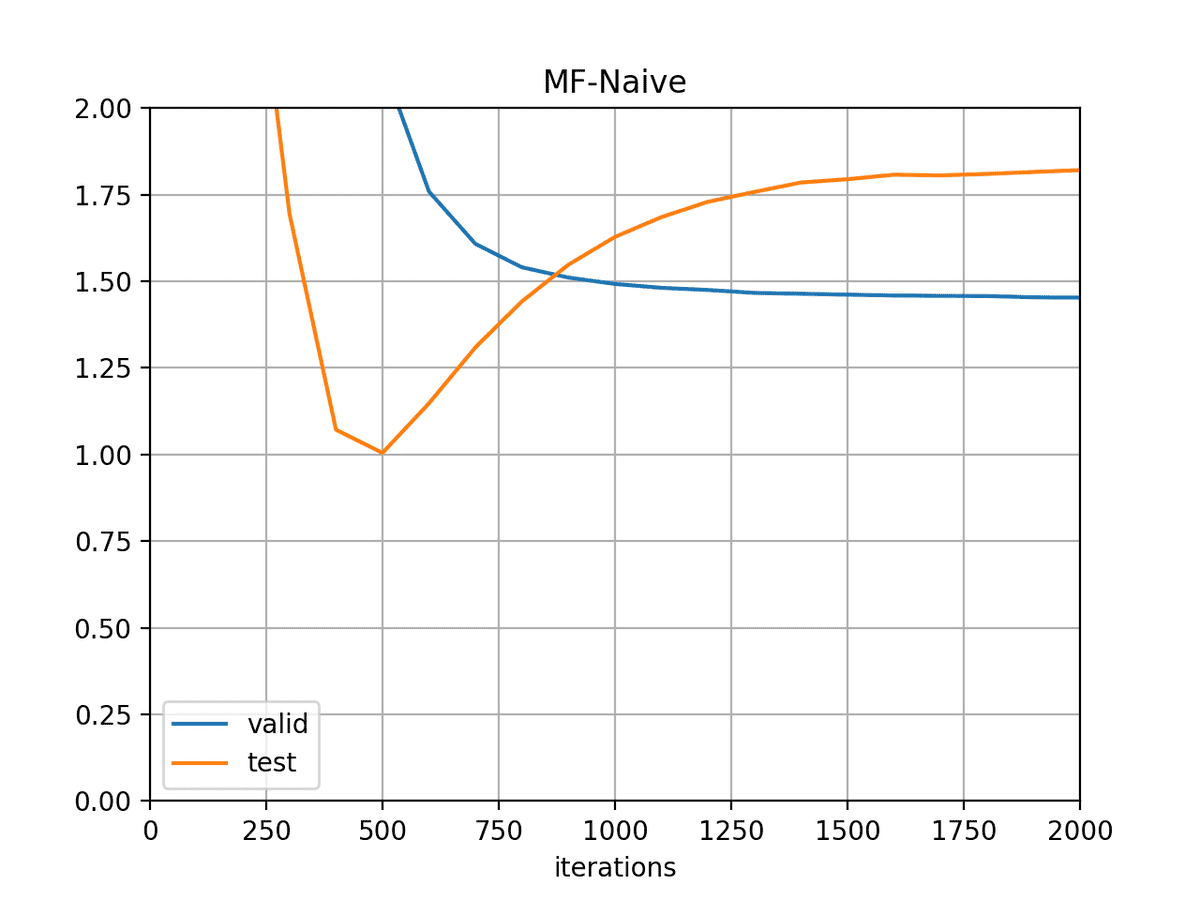
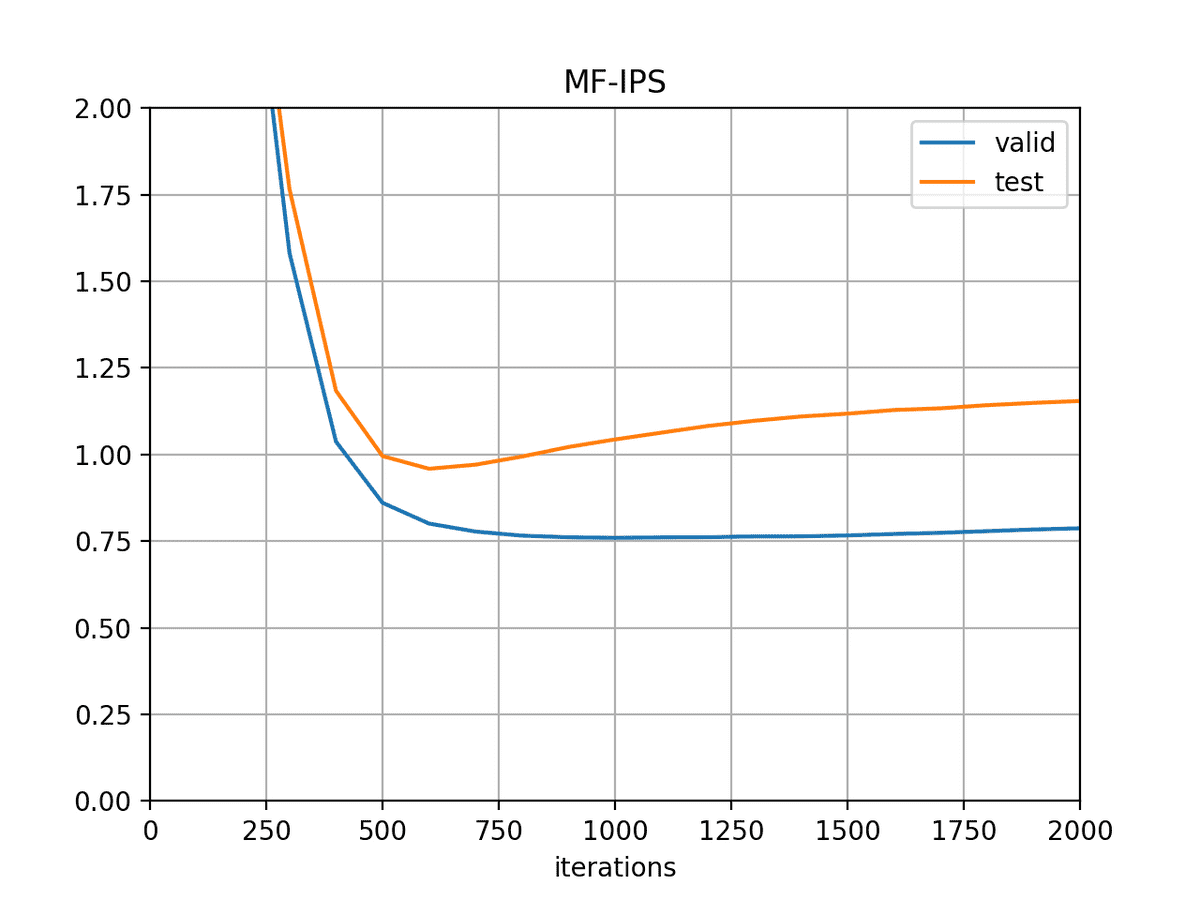
縦軸はMSE(mean squared error)(表記忘れ)。1枚目の学習曲線(MF-Naive)ではvalidationのlossが下がり切る前にtestのlossが大きく悪化(約1.8程度)している。 一方2枚目の学習曲線(MF-IPS)ではvalidationのlossが底についても約1.1弱と、大幅な改善が見られた。論文中では0.989と報告されていたので、あとはハイパラチューニングの問題か。

おわりに

今回紹介した論文はMCARなデータを必要とする手法でしたが、今年のSIGIR2020の論文Yuta Saito. Asymmetric Tri-training for Debiasing Missing-Not-At-Random Explicit Feedback. In SIGIR2020.ではMCARなデータが全くない状況を扱っているので必読です！ 数式や説明に間違いございましたらTwitterかコメント欄までお願い致します。

圧倒的参考資料たち

• Recent Topics on Counterfactual Machine Learning @usaito
• 因果推論で推薦システムを問い直す（評価指標編）@usaito
• Tobias Schnabel, Adith Swaminathan, Ashudeep Singh, Navin Chandak, and Thorsten Joachims. Recommendations as Treatments: Debiasing Learning and Evaluation. In ICML2016. pp. 1670–1679.
• Benjamin Marlin, Richard S. Zemel, Sam Roweis, Malcolm Slaney. Collaborative Filtering and the Missing at Random Assumption. In UAI2007, pp. 267–275.
• https://koumurayama.com/koujapanese/missing_data.pdf