ガウス過程回帰メモ(1)

$n$番煎じ感ありますが、「ガウス過程と機械学習」を読んだのでガウス過程回帰についてメモ。かなり五月雨式ではありますが。。。 ところどころコードも挟んでます。

線形回帰と次元の呪い

1次元の入力$x$について

という特徴ベクトルを考えれば

という線形回帰モデルとして表される。線形回帰については昔書いたのでこちら参照。

これについて一般化($\boldsymbol{\phi}(x) = (1, x, x^2, x^3)^{\mathrm{T}}$)すると

先程の式は4つの基底関数の重み付き和として見ることができる。 基底関数を$\phi_{h}(x) = \exp{\left( - \frac{\left(x - \mu_h \right)^2}{\sigma^2} \right)}$(ガウス基底関数)としたとき、

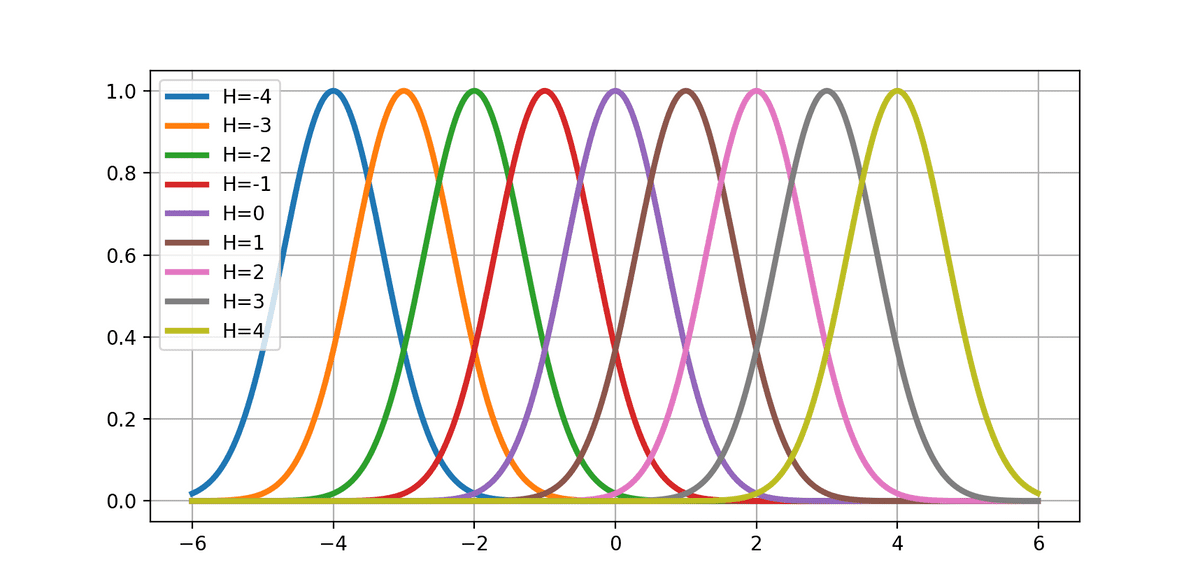
($\mu_h \in (-H, ..., -2, -1, 0, 1, 2, ..., H)$)

となる。

import numpy as np
import matplotlib.pyplot as plt

def phi_h(x: float, mu: float, sigma: float) -> float:
    return np.exp(- (x - mu) ** 2 / (sigma ** 2))

H: int = 4

for _mu in range(-H, H+1):
    x = np.arange(-6, 6, 0.01)
    y = np.vectorize(lambda x: phi_h(x, _mu, 1.0))(x)
    plt.plot(x, y, label=f"H={_mu}", linewidth=3)

plt.grid()
plt.legend()
plt.show()

とすると、下記のようなほとんど任意の形の関数が表される。 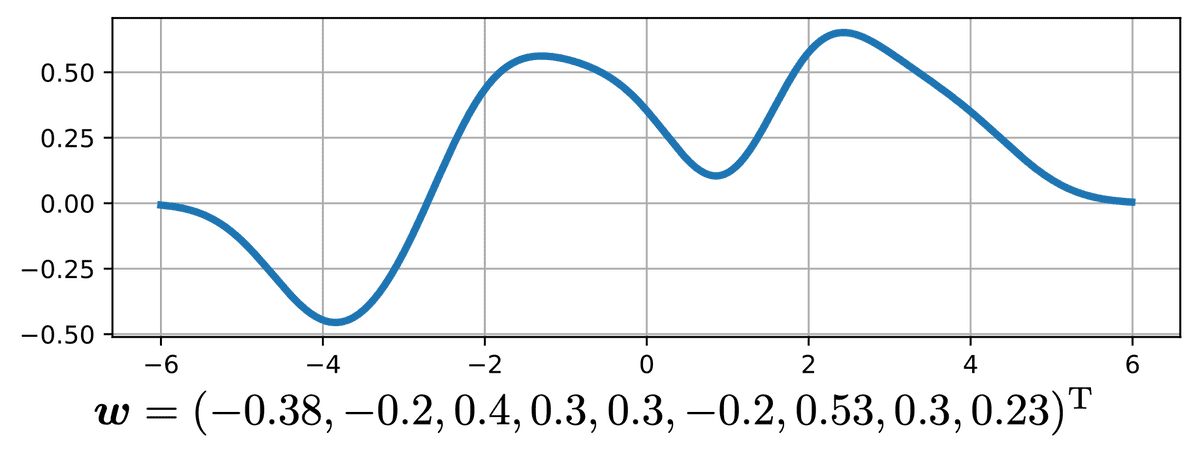この方法は動径基底関数回帰(radial basis function regression)という。

import numpy as np
import matplotlib.pyplot as plt

def phi_h(x: float, mu: float, sigma: float) -> float:
    return np.exp(- (x - mu) ** 2 / (sigma ** 2))

H: int = 4

x = np.arange(-6, 6, 0.01)
y: np.ndarray = np.zeros_like(x)

mu = range(-H, H+1)
w = [-0.38, -0.2, 0.4, 0.3, 0.3, -0.2, 0.53, 0.3, 0.23]

assert len(mu) == len(w), "ベクトルμとベクトルwの長さが異なります。"

for _mu, _w in zip(mu, w):
    y += _w * np.vectorize(lambda x: phi_h(x, _mu, 1.0))(x)

plt.plot(x, y, linewidth=3)
plt.grid()
plt.show()

一見すると任意の関数を表現することができそうなので良さそうだが、入力$\boldsymbol{x}$が1次元のとき、$H=10$としたとき重み$\boldsymbol{w}$の次元は $2H+1=21$次元。 これは基底関数の個数と同じ。

入力 $\boldsymbol{x}$ が2次元のとき、基底関数の個数は$21^2 = 441$。
入力 $\boldsymbol{x}$ が3次元のとき、基底関数の個数は$21^3 = 9261$…
入力 $\boldsymbol{x}$ が10次元のとき、基底関数の個数は$21^10=16679880978201$…
これを、次元の呪い(curse of dimensionality)という。

入力 $\boldsymbol{x}$ が2次元、$H=1$の例

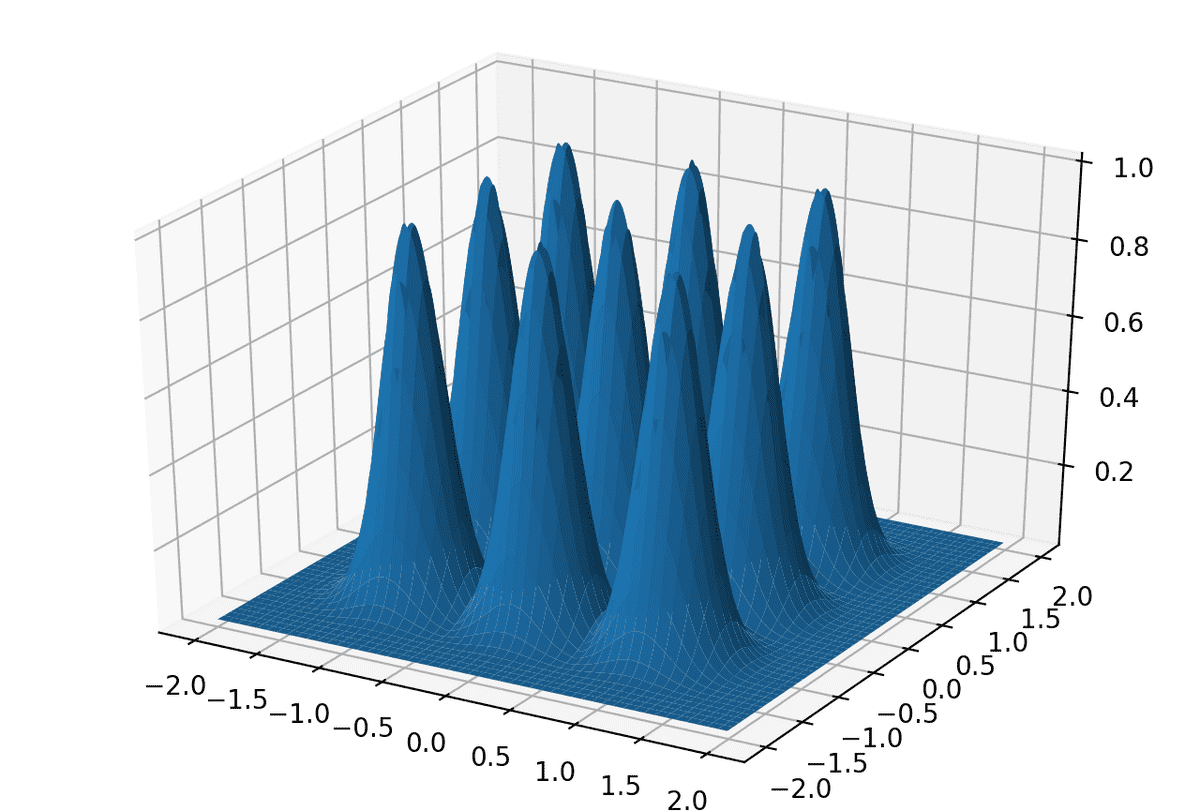
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def phi_h(x: float, mu: float, sigma: float) -> float:
    return np.exp(- (x - mu) ** 2 / (sigma ** 2))

H: int = 1
sigma: float = 0.3

x1 = np.arange(-(H+1), (H+1), 0.01)
x2 = np.arange(-(H+1), (H+1), 0.01)

xx1, xx2 = np.meshgrid(x1, x2)
yy = np.zeros_like(xx1)

fig = plt.figure()
ax = Axes3D(fig)

for mu1 in range(-H, H+1):
    for mu2 in range(-H, H+1):
        yy = np.maximum(yy, np.vectorize(lambda x: phi_h(x, mu1, sigma))(xx1) * np.vectorize(lambda x: phi_h(x, mu2, sigma))(xx2))

ax.plot_surface(xx1, xx2, yy)
plt.show()

ガウス過程

ということで無限次元の基底関数について無限次元の重み$\boldsymbol{w}$を計算するのは不可能なので、$\boldsymbol{w}$について事前分布を設け、$\boldsymbol{w}$期待値をとって積分消去することを考える。

入力 $\boldsymbol{x}$ について $\boldsymbol{x}$ の特徴ベクトルを

とするとN個の特徴ベクトルに対する線形回帰は下記のように表される。

ここで、計画行列$\Phi$は $x_1, \cdots x_N$が与えられれば定数行列となる。

重みがRidge Regressionと同様に $\boldsymbol{w} \sim \mathcal{N}(\boldsymbol{0}, \lambda^2 \boldsymbol{\mathrm{I}})$ に従うとき、 線形変換された $\boldsymbol{y} = \Phi \boldsymbol{w}$ もまたガウス分布に従う。 このとき、共分散行列は

となる。したがって、$\boldsymbol{y}$ の分布は多変量ガウス分布

となる。上記の式は、線形回帰モデルにあった重み $\boldsymbol{w}$ は期待値が取られて消えていることに注意。 つまり、$\boldsymbol{y}$ の分布はデータ数$\boldsymbol{N}$に依存する共分散行列$\lambda^2 \Phi \Phi^{\mathrm{T}}$によってきまることになる。

件の共分散行列を$\boldsymbol{\mathrm{K}} = \lambda^2 \Phi \Phi^{\mathrm{T}}$、$\boldsymbol{x}$ の特徴ベクトルを$\boldsymbol{\phi}(\boldsymbol{x}) = \left(\phi_0(\boldsymbol{x}), \phi_1(\boldsymbol{x}), \cdots, \phi_H(\boldsymbol{x}) \right)^{\mathrm{T}}$とすると、$(n, n^{\prime})$要素は

となる。つまり、2つの変数の共分散が大きいとは、似た値を取りやすいということなので、特徴量ベクトルの内積が大きい、すなわち特徴ベクトル空間において $x_n$ と $x_n$ が似ているなら、対応する$y_n$、$y_n$ も似た値を持つことになる。

参考書の中には、「ガウス過程の直感的な性質として入力 $\boldsymbol{x}$ が似ていれば、出力 $y$ も似ている」という旨が書かれていましたが、まさしくこのこと言っているのだと感じた。

参考書と同様に観測データ $\boldsymbol{y}$ は予め平均を引いておけば平均を $\boldsymbol{0}$ にできるので下記のガウス過程を扱う。

カーネルトリック

上の式によれば、$\boldsymbol{y}$ の分布は共分散行列 $K$ の要素、

だけで定まることがわかる。この値については結果さえ求まれば、$\boldsymbol{\phi}(\boldsymbol{x}_n)$ を明示的に求める必要はない(!!!!)。 $K_{nn^{\prime}}$ の値を与える関数を

$x_n$ と $x_n$ のカーネル関数(kernel function)とよび

と書く。

特徴ベクトル$\boldsymbol{\phi}(\boldsymbol{x})$を直接表現することを避け、カーネル関数だけで内積を計算することをカーネルトリック(kernel trick)と呼ぶ。

ガウス過程の定義

Definition 3.4 (ガウス過程の正確な定義) どんな自然数$N$についても、入力 $\boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_N \in \mathcal{X}$ に対応する出力のベクトル

$\boldsymbol{\mathrm{f}} = (f(\boldsymbol{x}_1), f(\boldsymbol{x}_2), \cdots f(\boldsymbol{x}_N))$

が平均

$\boldsymbol{\mu} = (\mu(\boldsymbol{x}_1), \mu(\boldsymbol{x}_2), \cdots, \mu(\boldsymbol{x}_N))$

と

$K_{nn'} = k(\boldsymbol{x}_n, \boldsymbol{x}_{n^{\prime}})$

を要素とする行列Kを共分散行列とするガウス分布 $\mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\mathrm{K}})$ に従うとき、 $f$ はガウス過程に従うといい、これを

$f \sim GP(\mu(\boldsymbol{x}), k(\boldsymbol{x}, \boldsymbol{x}^{\prime}))$

と書く。

ガウス過程からのサンプル

入力 $\boldsymbol{x}$ の間の類似度を図るためによく使われるガウスカーネル(Gaussian kernel)

についてサンプルを行ってみると下記のようなサンプルが得られる。 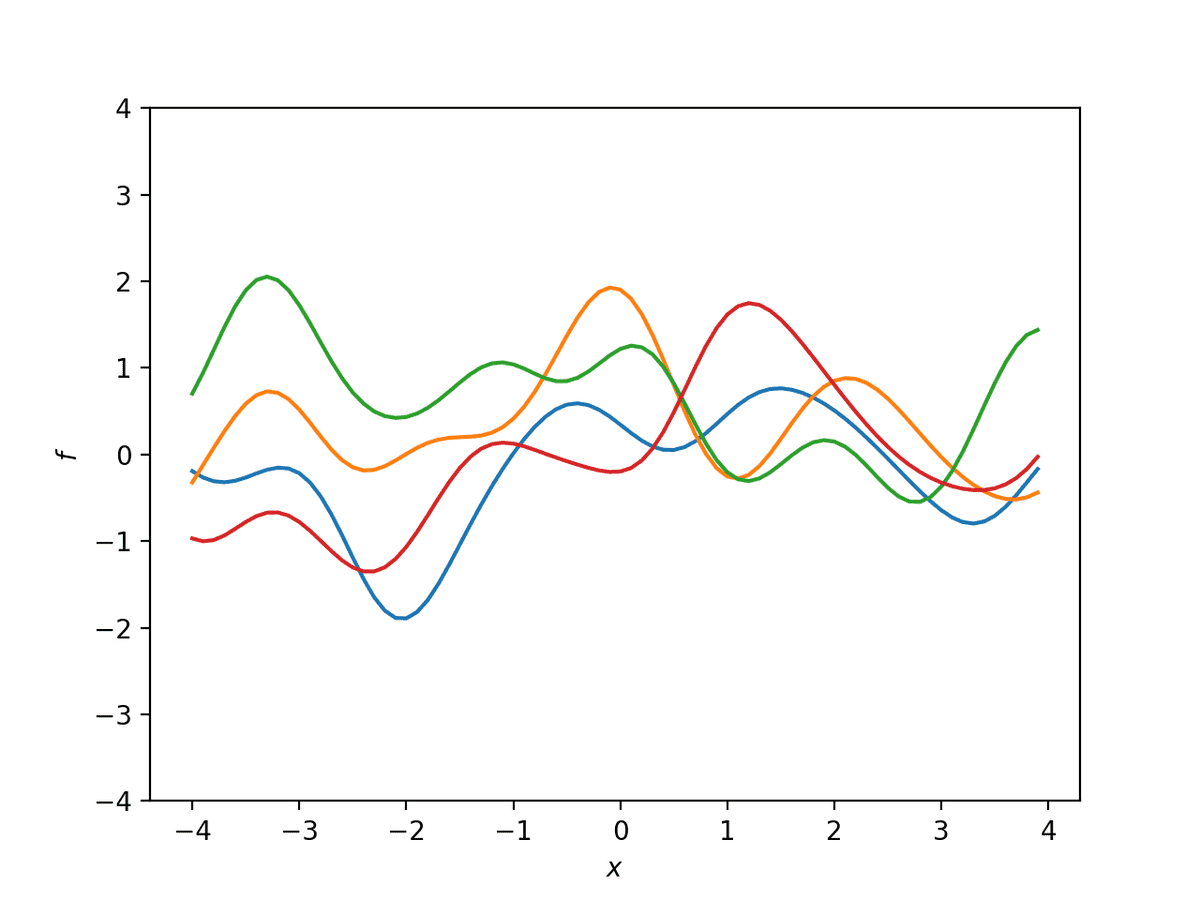また、このときの$K$を可視化すると、 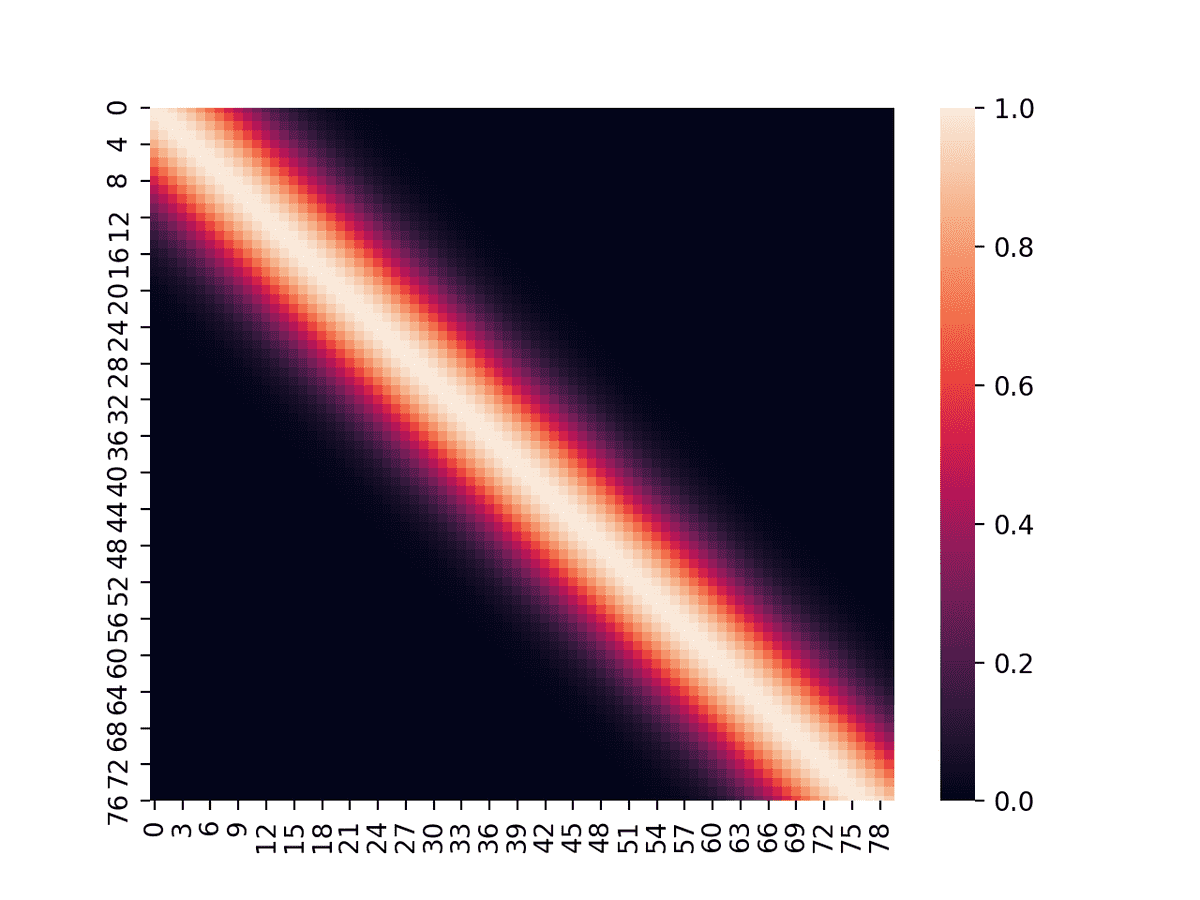となっており、近いデータ間の共分散が大きくなっていることがわかる。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns


def rbf(x1, x2, theta1=1.0, theta2=1.0):
    return theta1 * np.exp(- (x1 - x2)**2 / theta2)

x = np.arange(-4, 4, 0.1)[:, None]
zero = np.zeros(len(x))
K = np.zeros_like(x @ x.T)

for i in range(len(x)):
    for j in range(len(x)):
        K[i, j] = rbf(x[i], x[j])

for i in range(4):
    y = np.random.multivariate_normal(zero, K)
    plt.plot(x.flatten(), y)

plt.ylim([-4, 4])
plt.ylabel("$f$")
plt.xlabel("$x$")
plt.show()


print(np.linalg.eigvals(K+0.01+np.eye(len(K))))


sns.heatmap(K)
plt.show()