NNablaでLSTMの実装
January 28, 2018
今年二発目のエントリです。
NNablaでKerasっぽくLSTMを書きました。
Long Short-Term Memory (LSTM)
LSTMとは、前回実装したRNNだけでは取扱が困難だった系列データの長期依存を学習できるように改良した回帰結合型のニューラルネットワークである。
[Understanding LSTM networks](http://colah.github.io/posts/2015-08-Understanding-LSTMs/)より
詳しいアルゴリズムは上記サイトを参照。
細かい実装上のshapeを以下に示す。
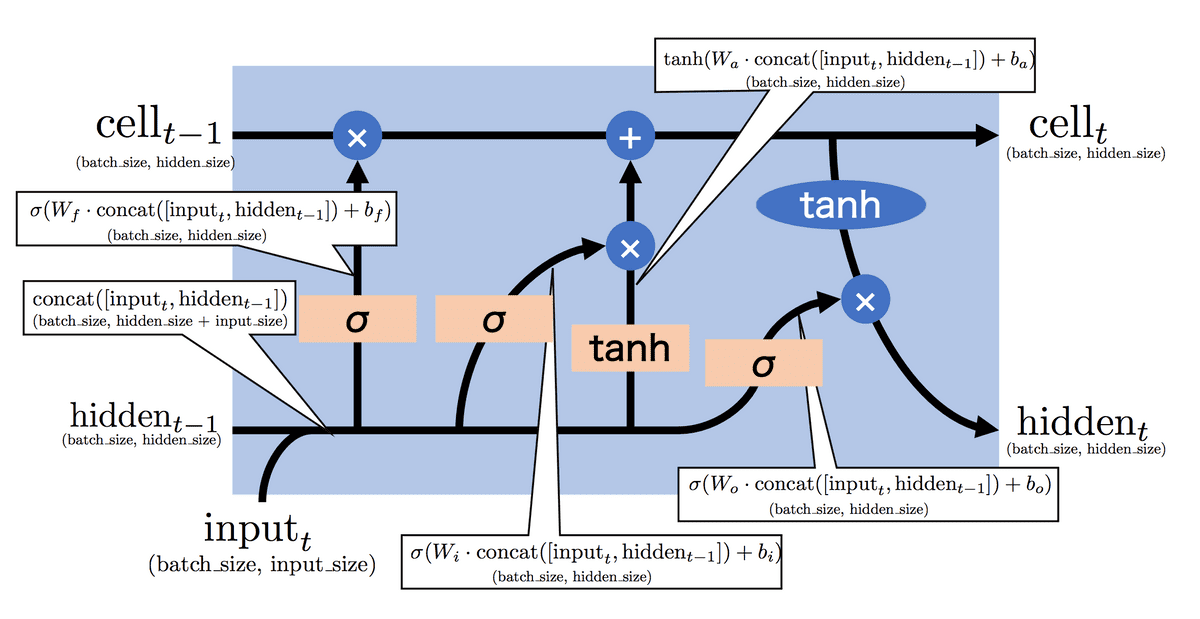
入力、忘却ゲート、入力ゲート、出力ゲートは以下のように示される。
これをNNablaで実装すると、
import nnabla as nn
import nnabla.parametric_functions as PF
import nnabla.functions as F
x_t = nn.Variable((batch_size, input_size))
hidden_prev = nn.Variable((batch_size, hidden_size))
_concat = F.concatenate(x_t, hidden_prev, axis=1)
a = F.tanh (PF.affine(_concat, hidden_size, name='Wa'))
input_gate = F.sigmoid(PF.affine(_concat, hidden_size, name='Wi'))
forget_gate = F.sigmoid(PF.affine(_concat, hidden_size, name='Wf'))
output_gate = F.sigmoid(PF.affine(_concat, hidden_size, name='Wo'))しかし、、、、は全て
、、、は全てであるから、実装上はこれらをconcatし、一回の行列演算で処理することができる。NNablaで実装すると、
import nnabla as nn
import nnabla.parametric_functions as PF
import nnabla.functions as F
x_t = nn.Variable((batch_size, input_size))
hidden_prev = nn.Variable((batch_size, hidden_size))
_concat = F.concatenate(x_t, hidden_prev, axis=1)
_hidden = PF.affine(_concat, 4*hidden_size, name='WaWiWfWo')
a = F.tanh (F.slice(_hidden, start=(0, hidden_size*0), stop=(batch_size, hidden_size*1)))
input_gate = F.sigmoid(F.slice(_hidden, start=(0, hidden_size*1), stop=(batch_size, hidden_size*2)))
forgate_gate = F.sigmoid(F.slice(_hidden, start=(0, hidden_size*2), stop=(batch_size, hidden_size*3)))
output_gate = F.sigmoid(F.slice(_hidden, start=(0, hidden_size*3), stop=(batch_size, hidden_size*4)))となる。 その後の処理は、
cell_t = input_gate * a + forgate_gate * cell_prev
hidden_t = output_gate * F.tanh(cell_t)となる。
前回のRNNと同様に書くと、最終的には以下のようになる。
import nnabla as nn
import nnabla.parametric_functions as PF
import nnabla.functions as F
def LSTMCell(x, c, h):
batch_size, units = c.shape
_hidden = PF.affine(F.concatenate(x, h, axis=1), 4*units, name='WaWiWfWo')
a = F.tanh (F.slice(_hidden, start=(0, units*0), stop=(batch_size, units*1)))
input_gate = F.sigmoid(F.slice(_hidden, start=(0, units*1), stop=(batch_size, units*2)))
forgate_gate = F.sigmoid(F.slice(_hidden, start=(0, units*2), stop=(batch_size, units*3)))
output_gate = F.sigmoid(F.slice(_hidden, start=(0, units*3), stop=(batch_size, units*4)))
cell = input_gate * a + forgate_gate * c
hidden = output_gate * F.tanh(cell)
return cell, hidden
def LSTM(inputs, units, initial_state=None, return_sequences=False, return_state=False, name='lstm'):
batch_size = inputs.shape[0]
if initial_state is None:
c0 = nn.Variable.from_numpy_array(np.zeros((batch_size, units)))
h0 = nn.Variable.from_numpy_array(np.zeros((batch_size, units)))
else:
assert type(initial_state) is tuple or type(initial_state) is list, \
'initial_state must be a typle or a list.'
assert len(initial_state) == 2, \
'initial_state must have only two states.'
c0, h0 = initial_state
assert c0.shape == h0.shape, 'shapes of initial_state must be same.'
assert c0.shape[0] == batch_size, \
'batch size of initial_state ({0}) is different from that of inputs ({1}).'.format(c0.shape[0], batch_size)
assert c0.shape[1] == units, \
'units size of initial_state ({0}) is different from that of units of args ({1}).'.format(c0.shape[1], units)
cell = c0
hidden = h0
hs = []
for x in F.split(inputs, axis=1):
with nn.parameter_scope(name):
cell, hidden = LSTMCell(x, cell, hidden)
hs.append(hidden)
if return_sequences:
ret = F.stack(*hs, axis=1)
else:
ret = hs[-1]
if return_state:
return ret, cell, hidden
else:
return ret
